ABUELITO DILE ADIÓS A LA DEPRESIÓN ¡JUEGA CON TU NIETO!
Los abuelos que tienen una estrecha relación con sus nietos suelen padecer menos depresiones, según ha mostrado un estudio liderado por la profesora asistente en el Departamento de Sociología y del Instituto sobre el Envejecimiento de la Universidad de Boston, Sara M. Moorman
TRADICIÓN ORIENTAL PARA PREDECIR EL SEXO DEL BEBÉ
La tabla china para predecir el sexo del bebé es uno de los sistemas más conocidos saber si esperas niño o niña. La predicción del sexo del bebé se realiza en China desde hace muchos años.
TU BEBE CON PAPERAS ¿QUE HACER?
Esta es una inflamación dolorosa de las glándulas salivales, que puede extenderse a otras glándulas del cuerpo. Las paperas afectan principalmente a niños y adolescentes, y es más grave en los pacientes que han pasado la pubertad.
¿SERÁ POSIBLE "LOS PASAPORTES DE INMUNIDAD" POR EL COVID-19?
Algunos gobiernos han sugerido que la detección de anticuerpos contra el SARS-CoV-2, el virus que causa COVID-19, podría servir como base para un "pasaporte de inmunidad" o "certificado libre de riesgos" que permitiría a las personas viajar o volver a trabajar
BASTA DE GANAR DINERO EN SUPLEMENTOS DE VITAMINAS Y MINERALES
Más de la mitad de los adultos en toman algún tipo de multivitamínico; muchos lo hacen con la esperanza de evitar enfermedades cardíacas, cáncer o incluso para mejorar su memoria. Pero un editorial publicado en los Anales de Medicina Interna dice que usar suplementos y multivitamínicos para prevenir enfermedades es una pérdida de dinero.
martes
LOS FÍSICOS DE PARTÍCULAS DESCONCIERTAN UNA NUEVA DUALIDAD
domingo
¿LA FÍSICA TEÓRICA ESTÁ DESPERDICIANDO NUESTRAS MEJORES MENTES VIVAS EN TONTERÍAS?
La historia de la física está llena de grandes ideas de las que has oído hablar, como el Modelo Estándar, el Big Bang, la Relatividad General, etc. Pero también está lleno de ideas brillantes de las que probablemente no haya oído hablar, como el modelo Sakata, la teoría del tecnicolor y el modelo de estado estacionario. y cosmología plasmática. Hoy, tenemos teorías que están muy de moda, pero sin ninguna evidencia de ellas: supersimetría, gran unificación, teoría de cuerdas y el multiverso.
Debido a la forma en que el campo está estructurado, sumido en una sinfonía de ideas, las carreras en física teórica de alta energía que se centran en estos temas a menudo tienen éxito. Por otro lado, elegir otros temas significa hacerlo solo. La idea de "belleza" o "naturalidad" ha sido un principio rector en física durante mucho tiempo, y nos ha llevado a este punto. En su nuevo libro, Lost in Math , Sabine Hossenfelder argumenta de manera convincente que continuar adhiriéndose a este principio es exactamente lo que nos lleva por mal camino.
El nuevo libro, Lost In Math, aborda algunas ideas increíblemente grandes, incluida la noción de que la física teórica está sumida en el pensamiento grupal y la incapacidad de confrontar sus ideas con la dura luz de la realidad, que no proporciona (hasta ahora) evidencia para respaldarlas. . (Sabine Hossenfelder / Libros básicos)Imagine que se le dio un problema hipotético de elegir dos multimillonarios de una lista y estimar la diferencia en su patrimonio neto. Imagina que son anónimos, y que no sabrás cuál vale más, dónde se ubican en la lista de multimillonarios de Forbes o cuánto vale realmente cualquiera de ellos en este momento.
Podemos llamar a la primera A , la segunda B , y la diferencia entre ellos C , donde A - B = C . Incluso sin ningún otro conocimiento acerca de ellos, hay una cosa importante que se puede afirmar sobre C : es muy poco probable que va a ser mucho, mucho más pequeño que una o B . En otras palabras, si A y B están en los miles de millones de dólares, entonces es probable que C también esté en los miles de millones, o al menos en los cientos de millones.
Cuando tiene dos números grandes, en general, y toma su diferencia, la diferencia será del mismo orden de magnitud que los números originales en cuestión. (E. Siegel / datos de Forbes)Por ejemplo, A podría ser Pat Stryker (# 703 en la lista), digamos, digamos, $ 3,592,327,960. Y B podría ser David Geffen (# 190), con un valor de $ 8,467,103,235. La diferencia entre ellos, o A - B , es entonces: $ 4,874,775,275. C tiene una oportunidad 50/50 de ser positiva o negativa, pero en la mayoría de los casos, va a ser del mismo orden de magnitud (en un factor de 10 o así) de ambos A y B .
Pero no siempre será así. Por ejemplo, la mayoría de los más de 2,200 multimillonarios en el mundo valen menos de $ 2 mil millones, y hay cientos de entre $ 1 mil millones y $ 1.2 mil millones. Si eligiera dos de ellos al azar, no lo sorprendería terriblemente si la diferencia en su patrimonio neto fuera solo de unas pocas decenas de millones de dólares.
Sin embargo, podría sorprenderte si la diferencia entre ellos era solo de unos pocos miles de dólares, o si era cero. "Qué improbable", pensarías. Pero podría no ser tan improbable después de todo.
Después de todo, no sabes qué multimillonarios estaban en tu lista. ¿Te sorprendería saber que los gemelos Winklevoss, Cameron y Tyler, los primeros multimillonarios de Bitcoin, tenían un patrimonio neto idéntico? ¿O que los hermanos Collison, Patrick y John (cofundadores de Stripe), valían la misma cantidad en unos pocos cientos de dólares?
No. Esto no sería sorprendente, y expone una verdad sobre los números grandes: en general, si A es grande y B es grande, entonces A - B también será grande ... pero no lo será si hay alguna razón por la cual A y B están muy juntos. Verá, la distribución de multimillonarios no es completamente aleatoria, por lo que podría haber alguna razón subyacente para que estas dos cosas aparentemente no relacionadas estén realmente relacionadas. (¡En el caso de Collisons o Winklevosses, literalmente!).
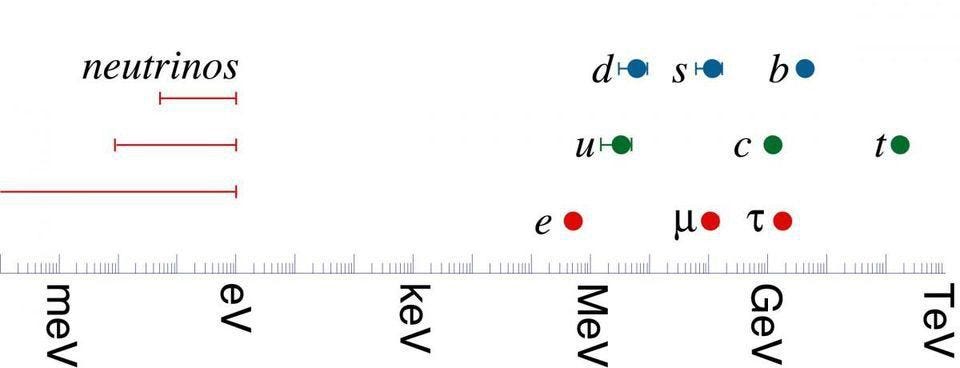
Esta misma propiedad es cierta en física. El electrón, la partícula más ligera que forma los átomos que encontramos en la Tierra, es más de 300,000 veces menos masivo que el quark top, la partícula del Modelo Estándar más pesada. Los neutrinos son al menos cuatro millones de veces más ligeros que el electrón, mientras que la masa de Planck, la denominada escala de energía "natural" para el Universo, es aproximadamente 10¹⁷ (o 100,000,000,000,000,000) más pesada que el quark top.
Si no conociera alguna razón subyacente por la que estas masas deberían ser tan diferentes, supondría que había alguna razón para ello. Y tal vez hay uno. Este tipo de pensamiento se conoce como un argumento de ajuste o "naturalidad". En su forma más simple, establece que debería haber algún tipo de explicación física de por qué los componentes del Universo con propiedades muy diferentes deberían tener esas diferencias entre ellos.

En el siglo XX, los físicos usaron argumentos de naturalidad con gran efecto. Una forma de explicar las grandes diferencias de escala es imponer una simetría a altas energías y luego estudiar las consecuencias de romperla a una energía más baja. Una serie de grandes ideas surgieron de este razonamiento, particularmente en el campo de la física de partículas. Los bosones de calibre en la fuerza de fuga eléctrica surgieron de esta línea de pensamiento, al igual que el mecanismo de Higgs y, como se confirmó hace solo unos años, el bosón de Higgs. Todo el Modelo Estándar se construyó sobre este tipo de simetrías y argumentos de naturalidad, y la naturaleza coincidió con nuestras mejores teorías.

Otro gran éxito fue la inflación cósmica. El Universo necesitaba haber sido afinado en gran medida en las primeras etapas para producir el Universo que vemos hoy. El equilibrio entre la tasa de expansión, la curvatura espacial y la cantidad de materia y energía dentro de ella debe haber sido extraordinaria; Parece ser antinatural. La inflación cósmica fue un mecanismo propuesto para explicarlo, y desde entonces se han confirmado muchas de sus predicciones , tales como:
- un espectro de fluctuaciones casi invariable en escala,
- la existencia de sobredensidades y subdensidades del súper horizonte,
- con imperfecciones de densidad que son de naturaleza adiabática,
- y un límite superior a la temperatura alcanzada en el Universo temprano posterior al Big Bang.

Pero a pesar del éxito de estos argumentos de naturalidad, no siempre dan fruto.
Hay una cantidad anormalmente pequeña de violación de PC en las fuertes desintegraciones. La solución propuesta (una nueva simetría conocida como la simetría de Peccei-Quinn) ha tenido cero de sus nuevas predicciones confirmadas. La diferencia en la escala de masa entre la partícula más pesada y la escala de Planck (el problema de la jerarquía) fue la motivación para la supersimetría; De nuevo, se ha confirmado cero de sus predicciones. La falta de naturalidad del Modelo Estándar ha llevado a nuevas simetrías en forma de Gran Unificación y, más recientemente, Teoría de Cuerdas, que (nuevamente) no ha confirmado ninguna de sus predicciones. Y el valor anormalmente bajo pero no nulo de la constante cosmológica ha llevado a las predicciones de un tipo específico de multiverso que ni siquiera se puede probar. Esto también, por supuesto, no está confirmado.

Sin embargo, a diferencia del pasado, estos callejones sin salida continúan representando los campos en los que los principales teóricos y experimentadores se agrupan para investigar. Estos callejones sin salida, que no han dado fruto literalmente para dos generaciones de físicos, continúan atrayendo fondos y atención, a pesar de estar posiblemente desconectados de la realidad por completo. En su nuevo libro, Lost In Math , Sabine Hossenfelder confronta hábilmente esta crisis, entrevistando a científicos convencionales, premios Nobel y contrarios (no chiflados) por igual. Puedes sentir su frustración, y también la desesperación de muchas de las personas con las que habla. El libro responde a la pregunta de "¿hemos dejado que las ilusiones sobre qué secretos guarda la naturaleza nublan nuestro juicio?" con un rotundo "¡sí!"

El libro es una lectura salvaje, profunda y estimulante que haría dudar a cualquier persona razonable en el campo que aún sea capaz de introspección. A nadie le gusta enfrentar la posibilidad de haber desperdiciado sus vidas persiguiendo el fantasma de una idea, pero de eso se trata ser teórico. Usted ve algunas piezas de un rompecabezas incompleto y adivina cuál es realmente la imagen completa; La mayoría de las veces te equivocas. Quizás, en estos casos, todas nuestras conjeturas han estado equivocadas. En mi intercambio favorito, entrevista a Steven Weinberg, quien se basa en su vasta experiencia en física para explicar por qué los argumentos de naturalidad son buenas guías para los físicos teóricos. Pero solo logra convencernos de que eran buenas ideas para las clases de problemas que anteriormente lograron resolver. No hay garantía de que sean buenas guías para los problemas actuales;
Si eres un físico teórico de partículas, un teórico de cuerdas o un fenomenólogo, especialmente si sufres de disonancia cognitiva, este libro no te gustará. Si eres un verdadero creyente en la naturalidad como la luz guía de la física teórica, este libro te irritará tremendamente. Pero si usted es alguien que no tiene miedo de hacer esa gran pregunta de "¿lo estamos haciendo todo mal", la respuesta podría ser un gran e incómodo "sí". Aquellos de nosotros que somos físicos intelectualmente honestos hemos estado viviendo con este malestar durante muchas décadas. En el libro de Sabine, Lost In Math , esta incomodidad ahora está disponible para el resto de nosotros.
Fuente: Medium, por Ethan Siegel.













